Динамічної нестійкості РУХУ ЗАРЯДЖЕНИХ ЧАСТИНОК У ПОСТІЙНОМУ НЕОДНОРІДНОМУ МАГНІТНОМУ ПОЛЕ
С.В. Поршнев
Нижньотагільський державний педагогічний інститут
Отримано 15 листопада 2000 р
Отримано чисельні рішення рівняння руху електричного заряду в постійному неоднорідному магнітному полі, параметри якого відповідають параметрам магнітного поля Землі. Виявлено існування хаотичних рішень рівнянь руху, отримані умови їх існування.
Питання про описі руху електричних зарядів (зокрема, обчисленні траєкторії) в постійному неоднорідному магнітному полі відноситься до числа класичних задач. Інтерес до неї стимулювався в першу чергу активними дослідженнями в галузі керованого термоядерного синтезу, де потрібно було знайти відповідь на питання про можливість утримання часток в магнітних пастках, що мають різні конфігурації магнітних полів [ 1 - 3 ]. Крім того, дана задача виникає в космічній астрофізиці [ 3 - 5 ] При поясненні причини існування радіаційних поясів у космічних тіл, які мають магнітним полем.
Для однозначного опису траєкторії руху нерелятівістского електричного заряду q в постійному неоднорідному магнітному полі напруженістю 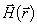 необхідно при заданих початкових умовах (
необхідно при заданих початкових умовах ( 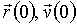 ) Вирішити систему рівнянь руху:
) Вирішити систему рівнянь руху:
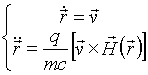 , (1)
, (1)
де m - маса заряду, 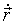 - радіус-вектор, проведений з початку координат в поточний стан заряду, з - швидкість світла.
- радіус-вектор, проведений з початку координат в поточний стан заряду, з - швидкість світла.
Необхідно відзначити, що аналітичні рішення системи диференціальних рівнянь другого порядку (1) вдається знайти лише для кількох випадків: 1) для постійного однорідного магнітного поля ( ![Необхідно відзначити, що аналітичні рішення системи диференціальних рівнянь другого порядку (1) вдається знайти лише для кількох випадків: 1) для постійного однорідного магнітного поля ( ), В якому заряд рухається по спіралі, тобто траєкторія руху являє собою суму двох рухів: обертання з рівномірною кутовою швидкістю по ларморовской окружності радіуса в площині, перпендикулярній до напрямку вектора напруженості магнітного поля , ( - проекція вектора швидкості на площину, перпендикулярну вектору ) І рівномірного переміщення уздовж вектора [ 3 ]; 2) для аксіально-симетричного магнітного поля, створюваного короткою котушкою з постійним електричним струмом (магнітної лінзи) [ 3 ]; 3) для неоднорідних магнітних полів, величина напруженості яких повільно змінюється уздовж шляху частинки [ 2 , 3 , 6 , 7 ]](/wp-content/uploads/2020/02/uk-dinamicna-nestijkist-ruhu-zaradzenih-castinok-v-postijnomu-neodnoridnomu-magnitnomu-poli-5.gif) ), В якому заряд рухається по спіралі, тобто траєкторія руху являє собою суму двох рухів: обертання з рівномірною кутовою швидкістю
), В якому заряд рухається по спіралі, тобто траєкторія руху являє собою суму двох рухів: обертання з рівномірною кутовою швидкістю  по ларморовской окружності радіуса
по ларморовской окружності радіуса 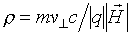 в площині, перпендикулярній до напрямку вектора напруженості магнітного поля
в площині, перпендикулярній до напрямку вектора напруженості магнітного поля  , (
, (  - проекція вектора швидкості
- проекція вектора швидкості  на площину, перпендикулярну вектору
на площину, перпендикулярну вектору 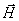 ) І рівномірного переміщення уздовж вектора
) І рівномірного переміщення уздовж вектора  [ 3 ]; 2) для аксіально-симетричного магнітного поля, створюваного короткою котушкою з постійним електричним струмом (магнітної лінзи) [ 3 ]; 3) для неоднорідних магнітних полів, величина напруженості яких повільно змінюється уздовж шляху частинки [ 2 , 3 , 6 , 7 ]. Умова повільності полягає в тому, що ларморовской радіус
[ 3 ]; 2) для аксіально-симетричного магнітного поля, створюваного короткою котушкою з постійним електричним струмом (магнітної лінзи) [ 3 ]; 3) для неоднорідних магнітних полів, величина напруженості яких повільно змінюється уздовж шляху частинки [ 2 , 3 , 6 , 7 ]. Умова повільності полягає в тому, що ларморовской радіус  повинен бути малий у порівнянні з розмірами області, в межах якої вектор напруженості магнітного поля помітно змінюється за величиною або за напрямком:
повинен бути малий у порівнянні з розмірами області, в межах якої вектор напруженості магнітного поля помітно змінюється за величиною або за напрямком:
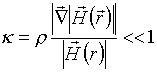 . (2)
. (2)
Відзначимо, що аналітичні рішення в другому і третьому випадках виявляються наближеними. Так, при розрахунку магнітних лінз передбачається, що магнітне поле, що діє на електричний заряд, зосереджено у відносно вузькій області простору, тобто в області руху заряду поздовжня складова напруженості магнітного поля 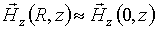 (
( 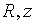 Циліндричні координати) залежать тільки від змінної z (z - відстань, що відраховується від центру магнітної котушки вздовж осі симетрії магнітного поля).
Циліндричні координати) залежать тільки від змінної z (z - відстань, що відраховується від центру магнітної котушки вздовж осі симетрії магнітного поля).
Завдання опису руху електричного заряду в слабо неоднорідному магнітному полі вирішується методом усереднення, званого "дрейфовим наближенням" [ 8 ]. Використовуючи цей метод, в [ 2 ] Показано, що рух електричного заряду в неоднорідному магнітному полі представляє суперпозицію наступних рухів:
1. Обертання по ларморовской окружності зі швидкістю 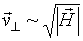 .
.
2. Руху центру ларморовской окружності уздовж силової лінії зі
c Коростів 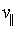 , при цьому
, при цьому  в силу закону збереження
в силу закону збереження
енергії.
3. дрейфовий рух центру ларморовской окружності зі швидкістю 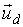 (
(  ||
|| 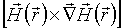 ),
),
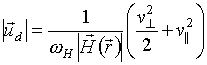 , (3)
, (3)
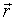 - радіус-вектор заряду,
- радіус-вектор заряду,  - ларморовской частота, відповідна напруженості магнітного поля в точці положення заряду.
- ларморовской частота, відповідна напруженості магнітного поля в точці положення заряду.
Інший підхід до вирішення даного завдання заснований на тому, що слабка неоднорідність магнітного поля породжує мало змінюються адіабатичні інваріанти, кількість яких збігається з числом ступенів свободи досліджуваної системи. Для даної задачі існування адіабатичних інваріантів обумовлено, кожним з перерахованих вище рухів [ 2 , 8 ]. Питання про збереження адіабатичних інваріантів найбільш докладно розглядалося для відкритих магнітних пасток: в [ 9 ] Отримано експериментальне підтвердження збереження адіабатичного інваріанту, пов'язаного з обертанням заряду по ларморовской окружності; в [ 10 ] Доведено вічне збереження даного адіабатичного інваріанту в ідеальній осесиметричною пастці з двовимірним рухом зарядів; в [ 11 ] Досліджено зміну інваріантів, обумовлене взаємодією трьох ступенів свободи.
Модель слабо неоднорідного поля прийнято також використовувати для пояснення руху заряджених частинок, захоплених магнітосферою Землі [ 2 , 3 , 8 ]. При цьому питання про адекватність даної моделі або не обговорюється [2,8], або наводиться оцінка параметра ![Модель слабо неоднорідного поля прийнято також використовувати для пояснення руху заряджених частинок, захоплених магнітосферою Землі [ 2 , 3 , 8 ]](/wp-content/uploads/2020/02/uk-dinamicna-nestijkist-ruhu-zaradzenih-castinok-v-postijnomu-neodnoridnomu-magnitnomu-poli-26.gif) для протонів і електронів з енергією 10 МеВ, що знаходяться в магнітному полі напруженістю 0,3 е [ 3 ]. Такий підхід, з нашої точки зору, не зовсім правомірний: по-перше, енергетичний спектр частинок, захоплених магнітосферою Землі, простягається від 100 кев до 100 МеВ. По-друге, в процесі руху відстань між зарядженою часткою і Землею буде змінюватися. З огляду на, сильну залежність напруженості геомагнітного поля від відстані (напруженість геомагнітного поля убуває відстанню по кубічному закону), видається більш правильним обчислювати значення коефіцієнта
для протонів і електронів з енергією 10 МеВ, що знаходяться в магнітному полі напруженістю 0,3 е [ 3 ]. Такий підхід, з нашої точки зору, не зовсім правомірний: по-перше, енергетичний спектр частинок, захоплених магнітосферою Землі, простягається від 100 кев до 100 МеВ. По-друге, в процесі руху відстань між зарядженою часткою і Землею буде змінюватися. З огляду на, сильну залежність напруженості геомагнітного поля від відстані (напруженість геомагнітного поля убуває відстанню по кубічному закону), видається більш правильним обчислювати значення коефіцієнта 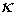 в кожній точці траєкторії руху заряду.
в кожній точці траєкторії руху заряду.
Інший не менш істотний недолік підходів до вирішення завдання про рух заряджених частинок в постійних неоднорідних магнітних полях, заснованих використанні дрейфового наближення та адіабатичних інваріантів, полягає в неможливості точного обчислення законів зміни координат частинки в часі і, як наслідок, неможливість детального опису особливостей руху і магнітотормозного випромінювання електричних зарядів. Зазначений недолік не дозволяє отримати відповіді і на інші не менш важливі з фізичної точки зору питання: чи існують у даної системи рівнянь ( 1 ) Хаотичні рішення, виявлені у багатьох динамічних систем, поведінка яких описується нелінійними диференціальними рівняннями [ 12 , 13 ]; за яких умов вони виникають; який механізм переходу від детермінованого поведінки до динамічного хаосу?
Метою даної роботи є дослідження особливостей руху електричних зарядів в постійних неоднорідних магнітних полях. Тут, в умовах відсутності точного аналітичного рішення системи нелінійних диференціальних рівнянь ( 1 ) Видається природним знаходити і аналізувати її чисельний розв'язок.
1. Математична модель руху зарядженої частинки в магнітному полі Землі
Як відомо [ 8 ], За своєю геометрії магнітне поле Землі виявляється близьким до поля магнітного диполя, нахиленого під кутом 11,5 ° до осі обертання Землі ( Мал. 1 ). Центр магнітного диполя зміщений приблизно на 400 км щодо центру Землі. У зв'язку з тим, що дана відстань виявляється значно менше радіуса Землі (6,4 × 103 км) далі в математичної моделі зазначеним зміщенням можна знехтувати і вважати, що магнітний диполь знаходиться на початку прямокутної декартової системи координат, вісь Оz, якої спрямована уздовж осі обертання Землі ( Мал. 1 ).
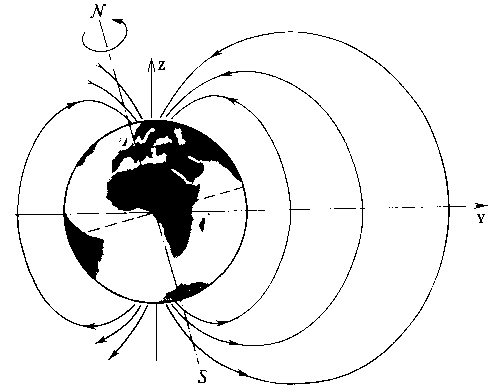
Рис.1.
Для отримання замкнутої системи диференціальних рівнянь необхідно доповнити систему рівнянь ( 1 ) Аналітичним виразом для напруженість магнітного поля диполя, яка має такий вигляд [ 14 ]:
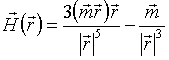 , (4)
, (4)
де 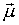 - вектор магнітного диполя,
- вектор магнітного диполя,  - радіус-вектор точки поточного становища електричного заряду. Завдання початкових умов: радіус-вектора
- радіус-вектор точки поточного становища електричного заряду. Завдання початкових умов: радіус-вектора 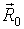 і початкової швидкості
і початкової швидкості  дозволяє вирішити задачу Коші для системи рівнянь руху ( 1 ).
дозволяє вирішити задачу Коші для системи рівнянь руху ( 1 ).
Для проведення подальших чисельних розрахунків зручно переписати систему диференціальних рівнянь ( 1 ) І вираз для напруженості магнітного поля ( 4 ) В безрозмірних змінних. В якості одиниць виміру відстані природно вибрати модуль радіус-вектора 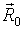 і модуль магнітного моменту
і модуль магнітного моменту  і ввести наступні безрозмірні змінні
і ввести наступні безрозмірні змінні  ,
,  (Як очевидно,
(Як очевидно, 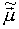 - одиничний вектор). У вибраних одиницях виміру рівняння (4) приймає наступний вигляд:
- одиничний вектор). У вибраних одиницях виміру рівняння (4) приймає наступний вигляд:
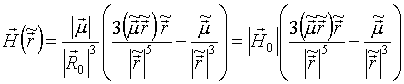 , (5)
, (5)
де 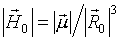 - модуль напруженості магнітного поля в точці початкового положення заряду.
- модуль напруженості магнітного поля в точці початкового положення заряду.
З (5) видно, що найбільш природно в якості одиниці вимірювання напруженості магнітного поля використовувати величину 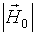 . Тоді вираз для безрозмірною напруженості магнітного поля
. Тоді вираз для безрозмірною напруженості магнітного поля  має такий вигляд
має такий вигляд
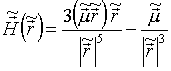 . (6)
. (6)
Вибравши в якості одиниць виміру часу 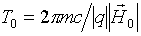 - період руху заряду по ларморовской окружності в магнітному полі в площині перпендикулярній вектору напруженості
- період руху заряду по ларморовской окружності в магнітному полі в площині перпендикулярній вектору напруженості  і використовуючи раніше введені безрозмірні змінні, можна записати систему рівнянь руху, що складається з 6 рівнянь, в наступному вигляді
і використовуючи раніше введені безрозмірні змінні, можна записати систему рівнянь руху, що складається з 6 рівнянь, в наступному вигляді
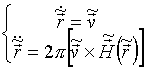 , (7)
, (7)
де безрозмірні початкові умови обчислюються за такими виразами:
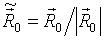 , (8)
, (8)
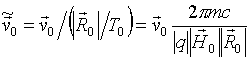 . (9)
. (9)
Відзначимо, що умова ( 2 ) В безрозмірних змінних приймає наступний вигляд:
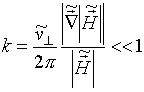 , (10)
, (10)
де 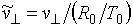 .
.
Аналіз виразів ( 6 ) - ( 9 ) Показує: 1) система безрозмірних рівнянь руху виявляється універсальною: коефіцієнти системи не залежать від конкретних параметрів заряду (маси і величини заряду) і напруженості магнітного поля; 2) безрозмірний радіус-вектор, проведений з початку координат в точку початкового положення заряду, - є одиничний вектор; 3) траєкторія руху заряду в постійному неоднорідному полі, створюваному магнітним диполем, визначається не окремими значеннями параметрів заряду і магнітного поля, але комбінацією цих параметрів: 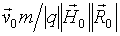 ; 3) при виконанні умови
; 3) при виконанні умови 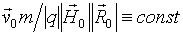 траєкторії руху електричних зарядів в постійних неоднорідних полях, створюваних магнітними диполями різної величини, виявляються однаковими; 4) для дослідження особливостей руху заряду в неоднорідному магнітному полі досить провести обчислення при різних значеннях безрозмірною початкової швидкості.
траєкторії руху електричних зарядів в постійних неоднорідних полях, створюваних магнітними диполями різної величини, виявляються однаковими; 4) для дослідження особливостей руху заряду в неоднорідному магнітному полі досить провести обчислення при різних значеннях безрозмірною початкової швидкості.
2. Особливості руху заряджених частинок в постійному неоднорідному магнітному полі
У зв'язку з тим, що найбільший практичний інтерес представляє рішення системи рівнянь ( 7 ) Для елементарних частинок, що рухаються в магнітних полях, що створюються космічними об'єктами, зокрема, в магнітному полі Землі, далі наводиться аналіз результатів чисельного моделювання руху протона, що знаходиться в геомагнітної пастці.
Для чисельного рішення системи рівнянь ( 7 ) Був використаний метод Рунге-Кутта 4-го порядку. Правильність роботи програми контролювалася за величиною кінетичної енергії заряду, яка в магнітному полі є інтегралом руху. При цьому виявилося, що максимальне значення відносної похибки обчислень не перевищувало 10-3%.
Безпосереднім результатом роботи програми є залежності відповідних декартових координат від часу (  ). наявність залежностей
). наявність залежностей  дозволяє провести обчислення значень параметра
дозволяє провести обчислення значень параметра 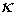 , Що характеризує неоднорідність магнітного поля, для кожної точки траєкторії, а також значень будь-якого з адиабатических інваріантів. Для аналізу особливостей руху заряду виявляється більш зручним використовувати залежність радіус-вектора заряду від часу (
, Що характеризує неоднорідність магнітного поля, для кожної точки траєкторії, а також значень будь-якого з адиабатических інваріантів. Для аналізу особливостей руху заряду виявляється більш зручним використовувати залежність радіус-вектора заряду від часу (  ). Це дозволяє проводити аналіз поведінки динамічної системи в двовимірному фазовому просторі замість аналізу в 6-ти мірному просторі.
). Це дозволяє проводити аналіз поведінки динамічної системи в двовимірному фазовому просторі замість аналізу в 6-ти мірному просторі.
Як приклад розглянемо результати розрахунків для наступних параметрів моделі: електричний заряд - протон (m = 1,672 × 10-24 г, q = 4,803 × 10-10 од. СГСЕ q); радіус-вектор початкового положення точкового заряду 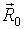 = (0,6,4 × 109,0) см; модуль напруженості магнітного поля
= (0,6,4 × 109,0) см; модуль напруженості магнітного поля  в точці з радіус-вектором
в точці з радіус-вектором  дорівнює 60 g (g = 10-5 е) [ 15 ]; вектор магнітного диполя
дорівнює 60 g (g = 10-5 е) [ 15 ]; вектор магнітного диполя 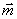 нахилений під кутом 11,5 ° до осі про Z ( Мал. 1 ). Обрані параметри, з одного боку, відповідають параметрам магнітного поля Землі на відстані, відраховувати від її центру, що дорівнює 10 радіусів Землі, з іншого, дозволяють виявити найбільш важливі особливості руху зарядів. Як змінюваного параметра моделі використовувалося абсолютне значення початкової швидкості заряду при незмінному напрямку вектора швидкості.
нахилений під кутом 11,5 ° до осі про Z ( Мал. 1 ). Обрані параметри, з одного боку, відповідають параметрам магнітного поля Землі на відстані, відраховувати від її центру, що дорівнює 10 радіусів Землі, з іншого, дозволяють виявити найбільш важливі особливості руху зарядів. Як змінюваного параметра моделі використовувалося абсолютне значення початкової швидкості заряду при незмінному напрямку вектора швидкості.
Аналіз залежностей R (t), отриманих при різних значеннях безрозмірною початкової швидкості та фіксованого в просторі орієнтації радіус-вектора, і нормованих амплітудно-частотних спектрів (далі спектрів) залежностей R (t) показав, що функція R (t) є деякою періодичної функцією , амплітуда якої залежить від величини безрозмірною початкової швидкості. (Типові залежності радіус-вектора заряду від часу, спектри функції R (t), а також залежно 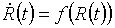 (Фазові траєкторії) представлені на Мал. 2 .)
(Фазові траєкторії) представлені на Мал. 2 .)
Ці результати показують, що траєкторія руху заряду в неоднорідному магнітному полі, створюваному магнітним диполем, в координатному просторі є фінітним квазіпериодичним рухом: заряд рухається по поверхні тора (радіус великому колу тора  , Радіус малого кола тора
, Радіус малого кола тора  ). Збільшення значення абсолютної швидкості призводить до збільшення радіусів великої і малої кіл тора. Даний висновок справедливий також для 6-ти мірного фазового простору, в якому рух заряду є квазипериодический рухом по поверхні 6-ти мірного тора. Цей результат зрозумілий: існування для кожного початкового умови тороидальной поверхні є наслідком збереження енергії заряду, що рухається в постійному магнітному полі.
). Збільшення значення абсолютної швидкості призводить до збільшення радіусів великої і малої кіл тора. Даний висновок справедливий також для 6-ти мірного фазового простору, в якому рух заряду є квазипериодический рухом по поверхні 6-ти мірного тора. Цей результат зрозумілий: існування для кожного початкового умови тороидальной поверхні є наслідком збереження енергії заряду, що рухається в постійному магнітному полі.
У зв'язку з тим, що найбільший інтерес представляють не окремі значення параметра 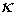 , Але його максимальна величина для даної траєкторії, а також непоодинокі значення адіабатичних інваріантів Ii, але параметри
, Але його максимальна величина для даної траєкторії, а також непоодинокі значення адіабатичних інваріантів Ii, але параметри  , Значення яких показує ступінь збереження інваріанта Ii, зазначені характеристики для різних значень початкової швидкості представлені в табл. 1 . (Тут разом зі значеннями безрозмірною початкової швидкості ми також вказуємо при вибраних параметрах магнітного поля значення відповідної кінетичної енергії, і обмежуємося величиною, що характеризує збереження адіабатичного інваріанту
, Значення яких показує ступінь збереження інваріанта Ii, зазначені характеристики для різних значень початкової швидкості представлені в табл. 1 . (Тут разом зі значеннями безрозмірною початкової швидкості ми також вказуємо при вибраних параметрах магнітного поля значення відповідної кінетичної енергії, і обмежуємося величиною, що характеризує збереження адіабатичного інваріанту  ). Крім зазначених величин в табл. 1 наведені значення радіусів великої і малої кіл тора.
). Крім зазначених величин в табл. 1 наведені значення радіусів великої і малої кіл тора.
Таблиця 1
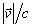
E, МеВ
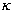
A,%
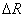
1.
0,3 × 10-2
4,22 × 10-3
2,0 × 10-3
1,6
0,014
2.
0,6 × 10-2
16,9 × 10-3
4,3 × 10-3
3,1
0,019
3.
1,2 × 10-2
67,5 × 10-2
1,3 × 10-2
6,4
0,028
4.
2,4 × 10-2
0,27
2,3 × 10-2
12,1
0,045
5.
4,8 × 10-2
1,08
8,1 × 10-2
23,5
0,078
6.
7,0 × 10-2
2,30
1,3 × 10-1
33,4
0,106
7.
9,0 × 10-2
3,80
1,7 × 10-1
42,1
0,129
8.
1,5 × 10-1
10,55
3,1 × 10-1
68,4
0,190
9.
2,0 × 10-1
18,76
4,4 × 10-1
82,9
0,228
10.
3,0 × 10-1
42,21
1,13
199,7
0,406
Аналіз результатів, представлених в табл. 1 показує, що збільшення безрозмірною швидкості руху заряду, що досягається збільшенням абсолютного значення швидкості при незмінних характеристиках магнітного поля, відбувається монотонне збільшення коефіцієнта 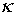 при одночасному руйнуванні адіабатичного інваріанту
при одночасному руйнуванні адіабатичного інваріанту  . При цьому виявляється, що точність збереження адіабатичного інваріанту А вже при значеннях
. При цьому виявляється, що точність збереження адіабатичного інваріанту А вже при значеннях 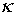 »9 × 10 -2, (тобто по усталеній думці б відповідала умовам застосовності дрейфового наближення
»9 × 10 -2, (тобто по усталеній думці б відповідала умовам застосовності дрейфового наближення 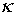 << 1) становить не більше 23,5%. Отже, використання моделі зберігаються адиабатических інваріантів для опису руху в магнітному полі Землі протонів з енергією більше 2 МеВ неправомірно. Більш того, як буде показано нижче, навіть для протонів, що мають значно менші кінетичні енергії, дана модель не дозволяє виявити ряд особливостей руху електричних зарядів в поле магнітного диполя.
<< 1) становить не більше 23,5%. Отже, використання моделі зберігаються адиабатических інваріантів для опису руху в магнітному полі Землі протонів з енергією більше 2 МеВ неправомірно. Більш того, як буде показано нижче, навіть для протонів, що мають значно менші кінетичні енергії, дана модель не дозволяє виявити ряд особливостей руху електричних зарядів в поле магнітного диполя.
Розглянемо більш докладно трансформацію спектрів залежностей R (t) і фазових траєкторій, отриманих по залежності R (t), при послідовному збільшенні значень безрозмірною початкової швидкості ( Мал. 2 ). при 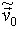 = (0,1,5 × 10-2,0) (
= (0,1,5 × 10-2,0) ( 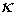 »2,1 × 10-3, А» 1,6%) рух частинки узгоджується з моделлю зберігаються адиабатических інваріантів: обертання частинки по ларморовской окружності, руху центру ларморовской окружності уздовж силової лінії, дрейфу центру ларморовской колу в площині XoY (рис. 2а ). Відзначимо, не торкаючись деталей, що тут і далі на рис. 2. внаслідок особливостей цифрових методів спектрального аналізу, детально розглянутих в [ 16 ], При обраних длительностях тимчасового інтервалу для пошуку рішення системи рівнянь руху ( 7 ) В спектрі функції R (t) не вдається вирішити гармоніки, відповідні найбільш повільного з перерахованих вище рухів - дрейфу частки в площині X про Y, оскільки на обраному часовому інтервалі укладається менш одного періоду дрейфового руху. Зазначений недолік легко усунути, збільшивши при незмінному кроці інтегрування часовий інтервал, на якому шукається рішення системи рівнянь руху ( 7 ). Однак цього не потрібно, оскільки, швидкість дрейфового руху при обраних початкових умовах (
»2,1 × 10-3, А» 1,6%) рух частинки узгоджується з моделлю зберігаються адиабатических інваріантів: обертання частинки по ларморовской окружності, руху центру ларморовской окружності уздовж силової лінії, дрейфу центру ларморовской колу в площині XoY (рис. 2а ). Відзначимо, не торкаючись деталей, що тут і далі на рис. 2. внаслідок особливостей цифрових методів спектрального аналізу, детально розглянутих в [ 16 ], При обраних длительностях тимчасового інтервалу для пошуку рішення системи рівнянь руху ( 7 ) В спектрі функції R (t) не вдається вирішити гармоніки, відповідні найбільш повільного з перерахованих вище рухів - дрейфу частки в площині X про Y, оскільки на обраному часовому інтервалі укладається менш одного періоду дрейфового руху. Зазначений недолік легко усунути, збільшивши при незмінному кроці інтегрування часовий інтервал, на якому шукається рішення системи рівнянь руху ( 7 ). Однак цього не потрібно, оскільки, швидкість дрейфового руху при обраних початкових умовах (  ) Виявляється значно менше швидкостей ларморовского обертання і руху центру ларморовской окружності, в чому легко переконається, записавши ( 3 ) В безрозмірному вигляді і врахувавши, що при обраних початкових умовах:
) Виявляється значно менше швидкостей ларморовского обертання і руху центру ларморовской окружності, в чому легко переконається, записавши ( 3 ) В безрозмірному вигляді і врахувавши, що при обраних початкових умовах:
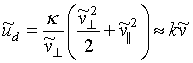 , (11)
, (11)
де 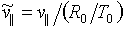 , Тому впливом зміщення, обумовленого дрейфом заряду, на особливості руху заряду в першому наближенні можна знехтувати.
, Тому впливом зміщення, обумовленого дрейфом заряду, на особливості руху заряду в першому наближенні можна знехтувати.
Аналіз залежності R (t) і відповідної фазової траєкторії при (0,0,3 × 10-2,0) дозволяє зробити висновок про існування у системи ( 7 ) Простого або регулярного атрактора. При цьому необхідно зазначити, особливість руху, не яка спостерігається при використанні моделі зберігаються адиабатических інваріантів. В спектрі функції R (t) крім гармонік, відповідним руху заряду уздовж силових ліній (f 1) і обертання заряду по ларморовской окружності (f 2), присутні дві додаткові гармоніки з частотами f 2 ± f 1. Їх існування обумовлене взаємодією розглянутих рухів: переміщення заряду вздовж силової лінії призводить до зміни швидкості обертання за ларморовской окружності внаслідок зміни напруженості магнітного поля.
для 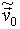 = (0,6,1 × 10-2,0) (
= (0,6,1 × 10-2,0) ( 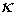 »1, 3 × 10-2, А» 6,4%) при збереженні в цілому регулярності аттрактора відбувається ускладнення руху: по-перше, з'являється подвоєна гармоніка (2 f 2), відповідна обертанню заряду по ларморовской окружності, по-друге, в спектрі крім описаних вище гармонік з'являються додаткові бічні гармоніки c з частотами f 2 ± 2 f 1, 2 f 2 ± f 1, 2 f 2 ± 2 f 1 ( Мал. 2б ). Даний результат обумовлений збільшенням "ступеня нелінійності" розглянутої динамічної системи: збільшення початкової швидкості заряду призводить до більш швидкого зміщення в область сильно неоднорідного магнітного поля, і, як наслідок, більшого взаємовпливу розглянутих рухів один на одного.
»1, 3 × 10-2, А» 6,4%) при збереженні в цілому регулярності аттрактора відбувається ускладнення руху: по-перше, з'являється подвоєна гармоніка (2 f 2), відповідна обертанню заряду по ларморовской окружності, по-друге, в спектрі крім описаних вище гармонік з'являються додаткові бічні гармоніки c з частотами f 2 ± 2 f 1, 2 f 2 ± f 1, 2 f 2 ± 2 f 1 ( Мал. 2б ). Даний результат обумовлений збільшенням "ступеня нелінійності" розглянутої динамічної системи: збільшення початкової швидкості заряду призводить до більш швидкого зміщення в область сильно неоднорідного магнітного поля, і, як наслідок, більшого взаємовпливу розглянутих рухів один на одного.
при 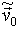 = (0, 1,23 × 10-1, 0) (
= (0, 1,23 × 10-1, 0) ( 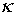 »2, 3 × 10-2, А» 12,1%) в спектрі з'являється додаткова гармоніка з частотою, рівній потроєною частоті обертання заряду по ларморовской окружності і бічних гармонік, що мають частоти 3 f 1 ± f 2. Подальше збільшення початкової швидкості призводить до збільшення амплітуди даних гармонік (див. Мал. 2г ). При початковій швидкості при
»2, 3 × 10-2, А» 12,1%) в спектрі з'являється додаткова гармоніка з частотою, рівній потроєною частоті обертання заряду по ларморовской окружності і бічних гармонік, що мають частоти 3 f 1 ± f 2. Подальше збільшення початкової швидкості призводить до збільшення амплітуди даних гармонік (див. Мал. 2г ). При початковій швидкості при 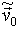 = (0, 3,59 × 10-1, 0) (
= (0, 3,59 × 10-1, 0) ( 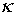 »1, 25 × 10-1, А» 33,4%) в спектрі з'являються гармоніки, що мають частоти 4 f 1 ± f 2, при подальшому збільшенні початкової швидкості повторюється описаний сценарій (див. Мал. 2д-2ж ).
»1, 25 × 10-1, А» 33,4%) в спектрі з'являються гармоніки, що мають частоти 4 f 1 ± f 2, при подальшому збільшенні початкової швидкості повторюється описаний сценарій (див. Мал. 2д-2ж ).
Найцікавіший результат виходить для початкових швидкостей, що перевищують за абсолютним значенням 0,3. Аналіз спектру функції R (t) при 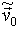 = (0, 1,54, 0) (
= (0, 1,54, 0) ( 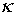 »1,1, А» 200%), представлений на рис. 2з, показує, що спектр функції стає безперервним. Траєкторія руху заряду в координатному просторі для даних початкових умов представлена на рис.3 , Залежність відстані між траєкторіями близькими в початковий момент часу представлена на рис.4 .
»1,1, А» 200%), представлений на рис. 2з, показує, що спектр функції стає безперервним. Траєкторія руху заряду в координатному просторі для даних початкових умов представлена на рис.3 , Залежність відстані між траєкторіями близькими в початковий момент часу представлена на рис.4 .
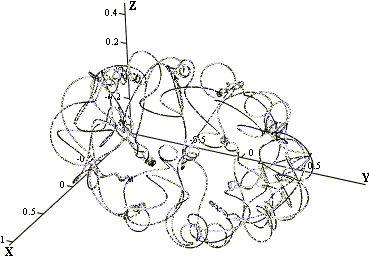
рис.3
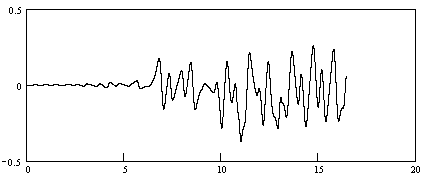
рис.4
З рис. 4 видно, що відстань між двома траєкторіями, стійкими по Пуассону, змінюється за випадковим законом, тобто рішення системи нелінійних диференціальних рівнянь ( 7 ) При даних початкових умовах виявляються нестійкими по Ляпунову. Таким чином, сукупність результатів, представлених на рис. 2з , 3 , 4 , Дозволяє зробити висновок про виникнення у досліджуваній системі динамічного хаосу за умови
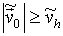 , (12)
, (12)
де 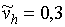 .
.
Особливо відзначимо, що отримані результати в повній мірі відносяться і до випадку руху в постійному неоднорідному магнітному полі заряджених частинок з релятивістськими швидкостями. Як відомо [17], рівняння руху в даному випадку має вигляд
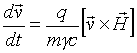 , (13)
, (13)
де
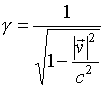 , (14)
, (14)
сила Лоренца, що діє на частинку спрямована так, що завжди  , Тому робота зовнішньої сили, пропорційна величині
, Тому робота зовнішньої сили, пропорційна величині 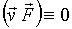 , Дорівнює нулю. Отже, енергія частинки, а разом з нею і абсолютне значення швидкості залишаються постійними. Тому можна сказати, що рух релятивістської частинки в постійному магнітному полі описується класичними рівняннями руху зарядженої частинки з постійною масою
, Дорівнює нулю. Отже, енергія частинки, а разом з нею і абсолютне значення швидкості залишаються постійними. Тому можна сказати, що рух релятивістської частинки в постійному магнітному полі описується класичними рівняннями руху зарядженої частинки з постійною масою  . Цей висновок дозволяє узагальнити отримані результати для частинок, що рухаються з релятивістськими швидкостями. Для цього при виборі одиниць виміру досить замінити у відповідних виразах масу частинки m на
. Цей висновок дозволяє узагальнити отримані результати для частинок, що рухаються з релятивістськими швидкостями. Для цього при виборі одиниць виміру досить замінити у відповідних виразах масу частинки m на  . З урахуванням цієї заміни вираз (9) набуває вигляду
. З урахуванням цієї заміни вираз (9) набуває вигляду
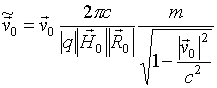 . (15)
. (15)
Підставивши вираз ( 12 ) В ( 15 ), Знайдемо абсолютне значення швидкості руху релятивістської зарядженої частинки в постійному неоднорідному магнітному полі, при якій виникає динамічний хаос:

 , (16)
, (16)
де
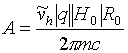 . (17)
. (17)
Підставивши, (16) в відомий вислів для енергії релятивістської частинки, отримаємо вираз для енергії, відповідної хаотичного руху
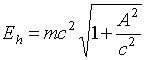 . (18)
. (18)
Для електронів, що рухаються в магнітного поле Землі, 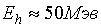 , Тобто рух електронів з енергією більшою
, Тобто рух електронів з енергією більшою  є хаотичним.
є хаотичним.
Висновок
У проведених численних дослідженнях особливостей руху електричних зарядів в постійному неоднорідному полі, створюваному магнітним діполяем, виявлені хаотичні рішення системи диференціальних рівнянь ( 1 ). Для магнітного поля, параметри якого відповідають параметрам магнітного поля Землі, визначені умови виникнення динамічного хаосу в даній системі і описаний механізм переходу до хаотичного режиму. Показано, що умови виникнення хаосу реалізуються для нерелятівістскіх протонів з кінетичної енергією ³ 84 МеВ і релятивістських електронів з енергією ³ 50 МеВ.
У той же час необхідно проведення подальших досліджень в цьому напрямку, зокрема, більш докладне дослідження структури хаосу: отримати чисельні оцінки показника Ляпунова, досліджувати можливість поява фрактальних структур і отримати оцінку їх розмірностей і ін.
ЛІТЕРАТУРА
1. Арцимович Л.А. Замкнені плазмові конфігурації. М.: Наука, 1969.
2. Арцимович Л.А., Сагдеев Р.З. Фізика плазми для фізиків. М .: Атомиздат, 1979.
3. Арцимовіч Л.А., Лук'янов С.Ю. Рух заряджених частинок в електричних і магнітних полях. М .: Наука, 1978.
4. Альвен Х. Космічна електродинаміка. М .: Изд-во іноземної літератури, 1952.
5. Пількенер С.Б. Основи космічної електродинаміки. М .: Физматгиз, 1961.
6. Сивухин Д.В .// Питання теорії плазми М .: Госатоміздат, 1963. Вип. 1. С. 7.
7. Морозов А.І., Соловйов Л.С .// Питання теорії Плазми М .: Госатоміздат, 1963. Вип. 2.
8. Заславський Г.М., Сагдеев Р.З. Введення в нелінійну фізику: Від маятника до турбулентності і хаосу. М .: Наука, 1988.
9. Родіонов М.С .// Атомна енергія. 1959. Т. 6. С. 623.
10. Арнольд В.І .// Доповіді АН СРСР. 1962. Т. 142. С. 758.
11. Чириков Б.В .// Питання теорії плазми. М .: Вища школа, 1983. Вип. 13. С. 3.
12. Аніщенко В.С. Складні коливання в простих системах: Механізми виникнення, структура і властивості динамічного хаосу в радіофізичних системах. М .: Наука, 1990..
13. Шустер Г. Детермінований хаос. Вступ. М .: Мир, 1988.
14. Тамм І.Є. Основи теорії електрики. М .: Наука, 1976.
15. Веденов А.А. Задачник з фізики плазми. М .: Атомиздат, 1981.
16. Марпл-мл. С.П. Цифровий спектральний аналіз та його додатки. М .: Світ, 1990..
17. Угаров В.А. Спеціальна теорія відносності. М .: Наука, 1977.
Автор:
Поршнев Сергій Володимирович, доктор технічних наук, доцент,
e-mail: [email protected] , Зав. кафедрою інформатики та обчислювальної техніки Нижнетагильского державного педагогічного інституту.


