анотація

А.В. Замятін, Е.А. Замятіна

У статті описаний алгоритм побудови розгортки не лінійчатих поверхонь-стей. Алгоритм реалізований за технологією ObjectARX для AutoCAD. Це дозволило інтегрувати алгоритм в AutoCAD. Розроблені алгоритми можуть бути використані в різних технічних завданнях, де існує необхідність побудови розгорток поверхонь.

Ключові слова: нелінійчатих поверхню, розгортка поверхні, метод тріангуляції

05.13.18 - Математичне моделювання, чисельні методи та комплекси програм

Багато поверхні, що застосовуються при проектуванні сучасних будинків і споруд, виготовляються з плоских матеріалів (метал, пластик, фанера і т.д.). Для виготовлення таких поверхонь необхідно виконати їх розгортку. У статті наведено алгоритм побудови умовної розгортки поверхонь методом тріангуляції [1, 2]. Алгоритм реалізований в середовищі ObjectARX для AutoCAD [3] на мові С ++ [4].

Розглянемо побудову умовної розгортки нелінійчатих поверхні методом тріангуляції. Нехай задана нелінійчатих поверхню мережею, що представляє собою два пересічних набору ліній li і mj (рис. 1).

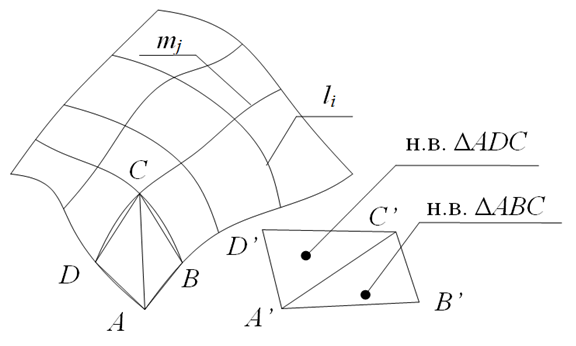
Мал. 1 Розгортка поверхні методом тріангуляції

Візьмемо відсік поверхні, обмежені криволінійними чотирикутником ABCD. Замінимо відрізки кривих, що обмежують заданий відсік, на відрізки прямих. Так як відрізки ліній мають невелику довжину, похибка буде невелика. Побудуємо діагональ AC чотирикутника. Знайдемо натуральну величину трикутника ABC - трикутник A 'B' C '(на рис. 1 ця натуральна величина про