Лекція № 3. Пряма

1. Проекції прямої

Для визначення прямої необхідні дві точки. Крапку визначають дві проекції на горизонтальну і фронтальну площині, т. Е. Пряма визначається за допомогою проекцій двох своїх точок на горизонтальній і фронтальній площинах.

На малюнку 17 показані проекції (а і a ?, b і b?) Двох точок А і В. З їх допомогою визначається стан деякої прямої АВ. При з'єднанні однойменних проекцій цих точок (т. Е. А і b, а? І b?) Можна отримати проекції аb і а? B? прямий АВ.

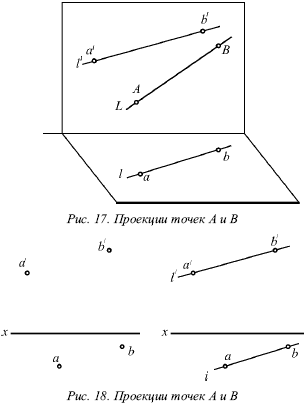
На малюнку 18 показані проекції обох точок, а на малюнку 19 - проекції проходить через них прямої лінії.

Якщо проекції прямої визначаються проекціями двох її точок, то вони позначаються двома поруч поставленими латинськими буквами, відповідними позначеннями проекцій точок, взятих на прямий: з штрихами для позначення фронтальної проекції прямої або без штрихів - для горизонтальної проекції.

Якщо розглядати не окремі точки прямої, а її проекції в цілому, то дані проекції позначаються цифрами.

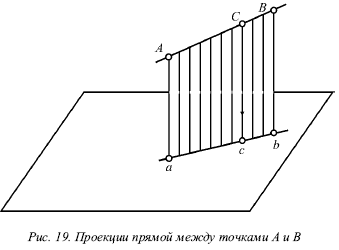
Якщо деяка точка С лежить на прямій АВ, її проекції з і з? знаходяться на однойменних проекціях прямої ab і а? b? . Дану ситуацію пояснює малюнок 19.

2. Сліди прямої

Слід прямий - це точка перетину її з деякою площиною або поверхнею (рис. 20).

Горизонтальним слідом прямої називається деяка точка H, в якій пряма зустрічається з горизонтальною площиною, а фронтальним - точка V, в якій дана пряма зустрічається з фронтальним площиною (рис. 20).

На малюнку 21а зображений горизонтальний слід прямої, а її фронтальний слід, - на малюнку 21б.

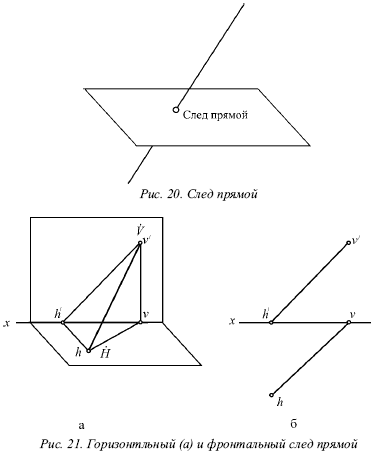
Іноді також розглядається профільний слід прямий, W - точка перетину прямої з профільної площиною.

Горизонтальний слід знаходиться в горизонтальній площині, т. Е. Його горизонтальна проекція h збігається з цим слідом, а фронтальна h? лежить на осі х. Фронтальний слід лежить у фронтальній площині, тому його фронтальна проекція ?? збігається з ним же, а горизонтальна v лежить на осі х.

Отже, H = h, і V = ??. Отже, для позначення слідів прямої можна застосовувати літери h і ??.

3. Різні положення прямої

Пряму називають прямою загального положення, якщо вона не паралельна і не перпендикулярна ні однієї площини проекцій. Проекції прямої загального положення теж не паралельні і не перпендикулярні осях проекцій.

Прямі, які паралельні одній з площин проекцій (перпендикулярні одній з осей). На малюнку 22 показана пряма, яка паралельна горизонтальній площині (перпендикулярна осі z), - горизонтальна пряма; на малюнку 23 показана пряма, яка паралельна фронтальній площині (перпендикулярна осі у), - фронтальна пряма; на малюнку 24 показана пряма, яка паралельна профільної площини (перпендикулярна осі х), - профільна пряма. Незважаючи на те що кожна з даних прямих утворює з однією з осей прямий кут, вони не перетинають її, а тільки схрещуються з нею.

Через те що горизонтальна пряма (рис. 22) паралельна горизонтальній площині, її фронтальна і профільна проекції будуть паралельні осях, що визначає горизонтальну площину, т. Е. Осях х та у. Тому проекції a? B? || х і a? b? || у, т. е. вони перпендикулярні осі z. Горизонтальна проекція ab може займати будь-яке положення на епюрі.

У фронтальній прямий (рис. 23) проекції аb || x і a? b? || z, т. е. вони перпендикулярні осі у, а тому в цьому випадку фронтальна проекція а? b? прямий може займати довільне положення.

У профільній прямій (рис. 24) аb || у, а? b || z, і обидві вони перпендикулярні осі х. Проекція а? B? може розташовуватися на епюрі будь-яким чином.

При розгляді тієї площині, яка проектує горизонтальну пряму на фронтальну площину (рис. 22), можна помітити, що вона проектує цю пряму і на профільну площину, т. Е. Вона є площиною, яка проектує пряму відразу на дві площини проекцій - фронтальну і профільну. Виходячи з цього її називають двічі проецирующей площиною. Таким же чином для фронтальної прямої (рис. 23) двічі проектує площину проектує її на площині горизонтальній і профільної проекцій, а для профільної (рис. 23) - на площині горизонтальній і фронтальній проекцій.

Дві проекції не можуть визначити пряму. Дві проекції 1 і 1? профільної прямої (рис. 25) без уточнення на них проекцій двох точок цієї прямій не визначать положення даної прямої в просторі.

У площині, яка перпендикулярна двом заданим площинах симетрії, можливе існування незліченної безліч прямих, для яких дані на епюрі 1 і 1? є їх проекціями.

Якщо точка знаходиться на прямій, то її проекції у всіх випадках лежать на однойменних проекціях цієї прямої. Зворотне положення не завжди справедливо для профільної прямої. На її проекціях можна довільним чином вказати проекції певної точки і не бути впевненим в тому, що ця точка лежить на даній прямій.

У всіх трьох окремих випадках (рис. 22, 23 і 24) положення прямої по відношенню до площини проекцій довільний її відрізок АВ, взятий на кожній з прямих, проектується на одну з площин проекцій без спотворення, т. Е. На ту площину, якій він паралельний. Відрізок АВ горизонтальної прямої (рис. 22) дає проекцію в натуральну величину на горизонтальну площину (аb = АВ); відрізок АВ фронтальної прямої (рис. 23) - в натуральну величину на площину фронтальної площини V (a? b? = AB) і відрізок АВ профільної прямої (рис. 24) - в натуральну величину на профільну площину W (a? b? = АВ), т. е. представляється можливим виміряти на кресленні натуральну величину відрізка.

Інакше кажучи, за допомогою епюр можна визначити натуральні розміри кутів, які розглянута пряма утворює з площинами проекцій.

Кут, який складає пряма з горизонтальною пло кісткою Н, прийнято позначати буквою?, З фронтальним площиною - буквою?, З профільної площиною - буквою?.

Будь-яка з розглянутих прямих не має сліду на паралельній їй площині, т. Е. Горизонтальна пряма не має горизонтального сліду (рис. 22), фронтальна пряма не має фронтального сліду (рис. 23), а профільна пряма - профільного сліду (рис. 24 ).

4. Взаємне розташування двох прямих

Можливі три випадки розташування прямих у просторі:

1) прямі присікаються, т. Е. Мають спільну точку;

2) прямі паралельні, т. Е. Не мають спільної точки, але лежать в одній площині;

3) прямі схрещуються, т. Е. Чи не лежать в одній площині, т. Е. Через них не можна провести площину.

Коли прямі перетинаються, на епюрі точки перетину їх однойменних проекцій на горизонтальній і фронтальній площинах знаходяться на одному перпендикуляр до осі х.

Розглянемо прямі I і II, які перетинаються в точці А (рис. 26). Спроектуємо обидві прямі на горизонтальну площину. Якщо врахувати, що точка А належить обом прямим, то її проекція а буде належати також і обидва проекція прямих.

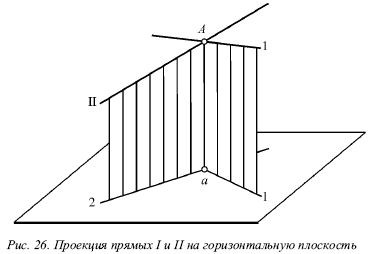
Схожа картина буде і на фронтальній площині, т. Е. Ці точки перетину однойменних проекцій а й а? є проекціями деякої точки А, і тому вони повинні лежати на одному перпендикуляр до осі х. Точно так же буде вірним і зворотне твердження: якщо на епюрі точки перетину однойменних проекцій прямих на дві площини (горизонтальну і фронтальну) лежать на одному перпендикуляр до осі х, то ці прямі перетинаються.

Нехай проекції прямих I до II (рис. 27) підкоряються цій умові.

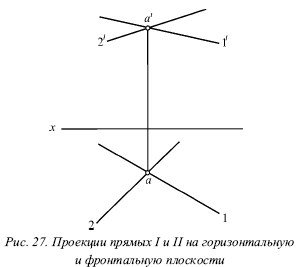
Тоді точки перетину їх однойменних проекцій можна Рассматриваються як проекції деякої точки в просторі. Позначимо точку перетину горизонтальних проекцій 1 і 2 буквою а, а точку перетину фронтальних проекцій 1? і 2? - буквою а? . Вже згадана точка А знаходиться і на прямий I, і на прямій II. Тобто вона є їхньою спільною точкою, в якій перетинаються ці прямі.

Пряме твердження справедливо у всіх випадках без винятку. Зворотне ж твердження можна застосувати в тому випадку, якщо хоча б одна з прямих профільна.

Коли прямі паралельні, на епюрі їх однойменні проекції паралельні (рис. 28).

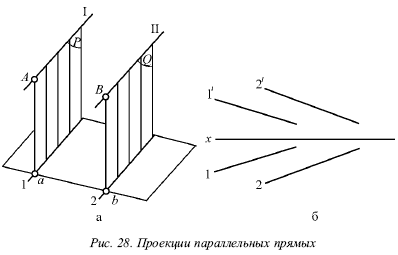
Насправді, площині Р і Q, що проектують прямі I і II на горизонтальну площину, паралельні, так як в кожній з цих площин можна вказати дві пересічні прямі, паралельні двом пересічним прямим другої площини, т. Е. Пряма I паралельна прямій II, і проектує промінь Аа паралельний променю Вb. Але дві паралельні площини Р і Q перетнуть горизонтальну площину. В результаті цього утворюються дві паралельні прямі 1 і 2, т. Е. Горизонтальні проекції прямих I і II паралельні між собою.

Аналогічно можна довести, що і будь-які інші однойменні проекції обох прямих також будуть паралельні один одному.

Вірно і зворотне твердження: прямі паралельні, якщо на епюрі їх однойменні проекції паралельні.

Якщо відомо, що горизонтальні і фронтальні проекції прямих I і II паралельні, буде справедливо наступне: 1 || 2 і 1? || 2? (Рис. 29).

В цьому випадку можна сказати, що площині Р I і Р II, що проектують прямі I і II на горизонтальну площину, паралельні, так як в цих площинах можна вказати по парі пересічних відповідно паралельних прямих (прямі 1 і 2 і проектують промені). Аналогічно площині Q I і Q II будуть паралельні.

Пряма I знаходиться в перетині площин Р I і Q I, а пряма II - в перетині площин РII QII. Звідси отримуємо, що пряма I паралельна площині РII, тому що знаходиться в площині, їй паралельної. Однак пряма I паралельна і площині Q II. Тому пряма I паралельна лінії перетину площин Р II і Q II, т. Е. Прямої II.

Доказ зворотного твердження не має сенсу для профільних прямих. Це пояснюється тим, що тоді замість двох площин, що проектують пряму на горизонтальну і фронтальну площини, існує тільки одна, двічі проектує площину (рис. 30).

Видно, що незалежно від розташування двох профільних прямих I і II в просторі їх горизонтальні і фронтальні проекції завжди паралельні (або зливаються).

Прямі будуть перехресними, якщо вони не паралельні і не перетинаються. Це випливає з того, що можливі тільки три випадки взаємного розташування прямих.

Для перехресних прямих справедливі твердження:

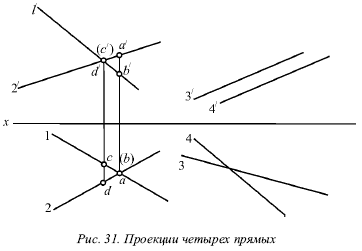
1) точки перетину однойменних проекцій на горизонтальній і фронтальній площинах чи не лежать на одному перпендикуляр до осі х (прямі I і II на рис. 31).

2) хоча б в одній парі однойменні проекції не паралельні (прямі III і IV на рис. 31).

Малюнок 31 показує проекції чотирьох прямих, будь-яка пара з яких схрещується.

Як і в розглянутих раніше випадках, зворотне твердження для перехресних прямих несправедливо за умови, що хоча б одна з прямих є профільною.

5. Перпендикулярні прямі

Розглянемо теорему: якщо одна сторона прямого кута паралельна площині проекцій (або лежить в ній), то прямий кут проектується на цю площину без спотворення.

Наведемо доказ для прямого кута ABC, одна сторона якого ВС паралельна горизонтальній площині (рис. 32).

Площина, в якій знаходиться сторона кута АВ і її проекція ab, перпендикулярна горизонтальній площині, так як містить перпендикуляр Вb до цієї площини. Пряма ВС перпендикулярна площині Q внаслідок її перпендикулярності двох пересічних прямих цій площині (АВ і Вb). Пряма bc паралельна ВС, т. Е. Вона також перпендикулярна Q, а значить і прямий ab, яка лежить в ній.

Ясно, що якщо на епюрі одна пара однойменних проекцій двох прямих перпендикулярна, а одна з двох інших проекцій паралельна осі х, то такі прямі утворюють в просторі прямий кут.

Припустимо, що ab? bc, b? з? || x.

Це показано на малюнку 33.

Можна провести через проекцію аb площину Q, що проектує пряму АВ на горизонтальну площину (рис. 33). Проекція bс перпендикулярна площині Q внаслідок того, що вона перпендикулярна двом прямим цій площині, т. Е. Проекції аb (за умовою), і проектується променю Вb як перпендикуляру горизонтальній площині.

Пряма ВС є паралельною горизонтальній площині, так як її фронтальна проекція bс паралельна осі х, тому вона паралельна своєї горизонтальної проекції, т. Е. Справедливий вираз ВС || bс. Отже, пряма ВС перпендикулярна площині Q і тому перпендикулярна прямий АВ незалежно від її положення в площині Q.

Через деяку точку М можна провести величезну кількість прямих, які перпендикулярні даній прямій АВ. Вони утворюють цілу площину Р, перпендикулярну АВ (рис. 34).

З усіх перпендикулярних прямих, які при цьому утворюються, тільки одна перетинає дану пряму. Це пряма MN, яка проходить через точку N перетину прямої АВ і площини Р.

Під перпендикуляром до прямої мається на увазі пряма, не тільки перпендикулярна даній прямій, але і перетинає на відміну від просто перпендикулярних перехресні прямі.

Прямий кут між перехресними прямими проектується на дану площину проекцій без спотворення, якщо одна з прямих паралельна цій площині або лежить в ній.